De Morganovy zákony

V praxi nejrozšířenější využití principu duality představují De Morganovy zákony, umožňují mechanicky určit duální funkce k negovanému součtu či součinu libovolného počtu proměnných, definovaných v přímém tvaru. Naproti tomu je duální výraz tvořen přímím součinem či součtem proměnných, které jsou vůči výrazu originálnímu definovány ve tvaru inverzním. de Morganovy zákony jsou tedy dva.
Platí:

Vidíme, že de Morganovy zákony definuji přímé duální funkce, levé i pravé strany rovnic jsou duální, každá popisuje zcela shodnou funkci, ale jiným způsobem.

Z definice zákonů je patrno určité omezeni. Na obou stranách rovnosti se vždy vyskytují všechny proměnné v jediném tvaru, bud přímém nebo negovaném a na každé straně je vždy jediný typ operátoru. Jak uvidíme dále, princip de Morganových zákonu lze snadno zobecnit pro libovolné logické výrazy.

Formát de Morganových zákonu je mimořádně vhodný k odvození a zapamatovaní dvou důležitých skutečností. Pro jejich zvýraznění jsme ve vztazích nahradili znaménka rovnosti šipkami.

Z postupu stanovení duálního výrazu zleva doprava je podle obou zákonů patrné že:

• každé hradlo NAND lze nahradit hradlem OR za předpokladu, že jeho vstupní signály budou negovány příslušnými invertory na vstupech.
• Každé hradlo NOR lze nahradit hradlem AND, opět doplněním příslušnými vstupními invertory.

   Pro doplnění je uveden i princip náhrady hradlem OR, AND hradly NOR, NAND pomocí negace vstupní funkce doplňkovým vstupním invertorem.

   Druhou praktickou zkušenost lze získat přiřazením schématickým symbolům duálních funkcí z pravé strany ke klasickým symbolům funkci NAND, NOR. Postup je jednoduchý. Symbol hradla NAND/NOR svým kroužkem (non) na výstupu udává, že jde o ekvivalent hradla AND/OR s invertorem na výstupu. Obdobně lze proto sestavit symboly duálních obvodů s hradlem OR/AND, nyní ovšem se znaky inverze na vstupech příslušného hradla.

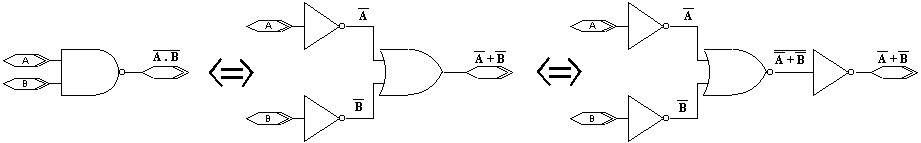
Tedy, libovolnou základní logickou funkcí lze definovat vždy dvěma symboly. Jeden z nich využívá součinového, druhý součtového hradla. Ačkoliv je jejich funkce zcela stejná, lze podle toho, zda je výstup symbolu přímý nebo invertovaný, naznačit (při kreslení schématu) nebo poznat (při jeho čtení), jakou úlohu má konkrétní hradlo v zapojení, zda je na jeho výstupu rozhodující dosažení hodnoty 0 (symbol NON) nebo 1 (přímý výstup). Pak je již, podle typu hradla (OR/AND) a přímého nebo invertovaného charakteru vstupu, snadné odvodit potřebnou podmínku ze strany vstupních signálů.

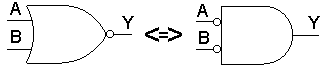
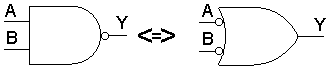
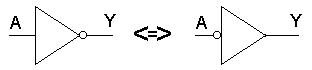
Stejně užitečná je i úprava symbolu invertoru. I když de Morganovy zákony názorně objasňují princip duality Booleovy algebry, nejsou ve své základní formě dostatečně univerzální, neumožňují přehlednou práci se složitějšími výrazy nebo proměnnými v obecném tvaru.