Shannonův teorém

Zobecněné využití principu duality, které si např. s de Morganovými zákony musíme odvozovat často velmi těžkopádně, definuje velmi jednoduše Shannonův teorém. Tento mimořádně praktický zákon umožňuje zcela mechanicky stanovit inverzní funkci libovolného výrazu podle vztahu:

   f [A, /B, C, ..., (+), (.)] = f [ /A, B, /C, ..., (.), (+)]

Inverzní logická funkce je z funkce původní odvozena tak, že:

• invertujeme každou původní proměnnou.
• vzájemně zaměňujeme všechny logické operátory.

   Zde je třeba jasně definovat, jaký je rozdíl mezi duální a inverzní funkcí. Zatímco duální funkce je jiným způsobem vyjádřená, avšak obsahově zcela shodná. Inverzní funkce je skutečnou inverzí původní funkce.

Jak vyplývá z definice de Morganových zákonů i Shannonova teorému, při vytváření duální i inverzní funkce se vzájemně mění disjukční výrazy na konjukční a opačně. Z toho vyplývá, že duální formou libovolného logického výrazu můžeme odvodit posloupností stanovení inverzní funkce a její následnou negací. Přitom lze funkce výhodně upravovat a zjednodušovat při dodržování pravidel Booleovy algebry. Navíc přistupuje nutnost věnovat zvýšenou pozornost prioritě logických operátorů. Násobení má přednost před sčítáním. Nejbezpečnější je před začátkem jakýchkoliv úprav zavést do výrazu explicitní závorky.Při inverzích složitých výrazů s několikastupňovými negacemi je nutné jejich postupné zjednodušení směrem zevnitř.
Postup při použití Shannonova teorému nejlépe osvětlí jednoduché příklady.

• Nejprve znovu ověříme 2. distributivní zákon:
  (A + C) . (B + C) = Y.
  Inverzí funkce podle Shannona získáme součtový tvar /A . /C + /B . /C = Y , který využitím 1. distributivního zákona upravíme /C (/A + /B) = /Y a nakonec zpětnou inverzí C + AB = Y získáme duální funkci a tedy důkaz správnosti.

• Také důkaz v opačném směru bude zcela jednoduchý: (AB) + C = Y Inverzi funkce (/A + /B) . /C = Y, po úpravě podle 1. distributivního zákona /A . /C + /B . /C = Y a opětovné inverzi získáme opět správný tvar duální funkce (A + C) . (B + C) = Y.

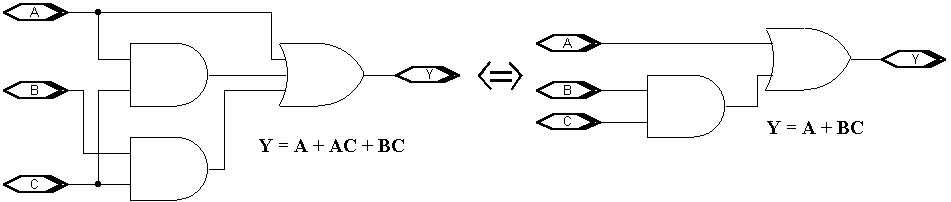
• Jako další příklad zkusme minimalizovat, nebo-li co nejvíce zjednodušit funkci A + AC + BC = Y. Nejprve z opatrnosti zavedeme prioritní závorky A + (AC) + (BC) = Y, pak vytknutím proměnné C upravíme A + C (A + B)= Y a určíme inverzní funkci /A (/C + /A . /B) = /Y. Protože /A . /A = /A, lze upravit /A . /C + /A . /B = /Y a po vytknutí /A (/B + /C) = /Y shledáváme, že výraz už dále zjednodušit nelze. Proto opětovnou inverzí zjistíme konečný tvar minimalizované funkce A + BC = Y. Porovnání realizace původní a minimalizované funkce s hradly AND a OR.

• Jako poslední příklad minimalizujeme různými postupy funkci Y = A + /A . /B, tj. disjukční funkci členů v přímém a inverzním tvaru:
  
  
  • bez předběžné úpravy negovaného součinu:
    Y = A + (/A . /B)
    /Y = /A . AB
    protože /A . A = 0
    /Y = 0 . B = 0
    je po opětovné inverzi
    Y = 1
    
    
  • s využitím úpravy /A . /B podle de Morganova zákona:
    Y = A + /A . /B
    Y = A + /A + /B
    protože A + /A = 1
    Y = 1 + B
    Y = 1

Vidíme, že v tomto případě nebylo třeba inverzní funkci vůbec hledat. Shannonův teorém umožňuje snadno odvodit inverzní tvar libovolné logické funkce. Ta je, díky vzájemné konverzi disjukčních a konjukčních tvarů, velmi užitečná pro přehledné úpravy a minimalizace logických výrazů i funkcí. Se znalostí dosud uvedených zákonů již lze vystačit při řešení mnoha praktických problémů v různých oblastech aplikace kombinačních obvodů. Bohužel, složitost jejich řešení, nepřehlednost a obtížnost algebraického popisu funkce exponenciálně narůstá s počtem proměnných v logické rovnici. Všimněme si ještě několika pravidel Booleovy algebry, nazývaných pravidly pohlcování, která často mohou logicky výraz podstatně zjednodušit:

• A + AB = A výsledek funkce je plně určen proměnnou A, na konjunkcí AB vůbec nezávisí.

• A (A + B) = A, zde je funkce určena konjunkcí A . A = A.

• (A + /B) B = AB, protože B . /B = 0, je funkce plně určena konjunkcí AB.

• A . /B + B = A + B, je-li proměnná A = 0, je funkce určena proměnnou B, je-li proměnná B = 0, je funkce určena proměnnou A.