Stavový diagram a pravdivostní tabulka sekvenčního obvodu

Stavový diagram umožňuje dokonale postihnout vzájemný vztah vnějších (známých nebo požadovaných) a vnitřních (hledaných) proměnných a stavů sekvenčního obvodu.

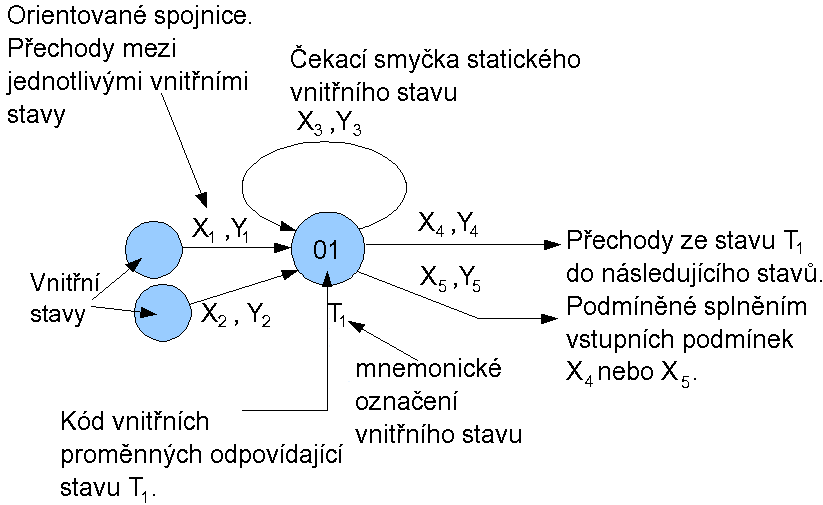
   Vnitřní stavy se v grafu označují kolečkem, jejich možné posloupnosti, představující akce obvodu, se označují šipkou orientovanými spojnicemi. Každý vnitřní stav může být bud' dynamický (trvá pouze jednu periodu hodinového signálu), nebo statický. Statický vnitřní stav v grafu naznačuje čekací smyčka. Její přechodová spojnice nesměřuje k dalšímu stavu, ale vrací se zpět na stav, z něhož vychází. Z tohoto stavu může být obvod vyveden pouze změnou vstupní proměnné (nebo počáteční podmínky).

Kritickou fází návrhu stavového diagramu je správné stanovení počtu vnitřních stavů. To je záležitostí důkladné analýzy zadání úlohy, odvození potřebných relací mezi vstupními a výstupními proměnnými. Z nich vyplývá počet vnějších akci (spojnic grafu) a tím i vnitřních stavů. Tato práce vyžaduje určitou zkušenost, kterou však lze získat velmi rychle. Každý klopný obvod (nebo paměťová buňka) je schopen vyjádřit dva vnitřní stavy (0, 1, tj. jednu vnitřní proměnnou).

Návrh sekvenčního obvodu tedy začíná analýzou úlohy a postupným sestavováním stavového diagramu. Začínáme v situaci, kdy jsme si udělali určitou představu o požadovaných vnějších akcích obvodu. K ním hledáme optimální počet a vazby vnitřních stavů jako funkce vstupních proměnných. Prakticky souběžně s návrhem grafu je vhodné začínat s vyplňováním pravdivostní tabulky. Osvědčený příklad jejího možného uspořádání znázorňuje následující obrázek.

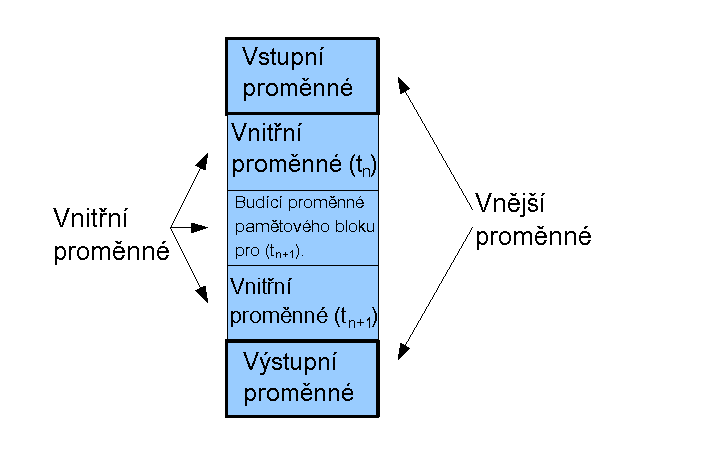
   Skládá se ze dvou hlavních poli. Pole vnějších proměnných jsou rozložena po obou okrajích tabulky. Nahoře je pole vstupních a dole výstupních proměnných. Počet sloupců pravdivostní tabulky je určen počtem vstupních a vnitřních proměnných obvodu. Jedna vnitřní proměnná může postihovat dva vnitřní stavy - obojí odpovídá jednomu klopnému obvodu (paměťové buňce). To znamená, má-li diagram pět vnitřních stavů, je pro jejich interpretaci v tabulce zapotřebí tři vnitřních proměnných, pro čtyři stavy dvou proměnných atd. Odtud vyplývá, že např. obvod s jednou vstupní proměnnou a čtyřmi vnitřními stavy = dvěma vnitřními proměnnými musí být v tabulce popsán 2¹⁺² = osmi sloupci, aby byly vyčerpány všechny jejich kombinace.

Mezi vnitřními stavy diagramu a vnitřními proměnnými v tabulce musí existovat přesná vzájemná souvislost. Stejná souvislost musí být zajištěna mezi vstupními a výstupními proměnnými tabulky a spojnicemi grafu, definujícími přechody od jednoho vnitřního stavu ke druhému. Konečným cílem společné konstrukce je úplné vyplnění pravdivostní tabulky, podle které může být navržen vlastni obvod.

Nyní již k postupu návrhu. Jednotlivé stavy diagramu si označíme pomocnými, nečíselnými identifikátory. Vhodné je buď slovní, písmenové nebo kombinované (písmeno + číslice) označeni. Jeden ze stavů považujeme za výchozí. Tomu stavu přísluší určité logické hodnoty vstupních a výstupních proměnných, které současně určuji vazbu tohoto stavu na stav další nebo na sebe sama. Zakreslíme tedy příslušnou orientovanou spojnici a popíšeme ji těmito hodnotami. Postupným vyčerpáním všech vazeb popíšeme celý stavový diagram. Pokud se jedná o sekvenční obvod, pracující v uzavřeném cyklu, bude i stavový diagram uzavřený, cyklický. Pro jednorázové funkce musí být diagram otevřený. To se řeší tak, že poslední stav je statický a "volá sám sebe".

Následuje přiřazení kombinace všech vnitřních proměnných (které budou v další fázi využity pravdivostní tabulkou) ke každému vnitřnímu stavu diagramu. Tyto kódy, které se většinou zapisují přímo do stavového kolečka, mohou být voleny libovolně. Většinou se však snažíme, pokud je to možné, aby se bud' co nejvíce blížily odpovídajícím hodnotám příslušných výstupních proměnných, nebo aby byly technicky snadno realizovatelné, např. jednoduchým čítačem nebo posuvným registrem. Tak se zjednodušují kombinační obvody.

Ve druhé fázi přepisujeme jednotlivé, vzájemně související vnější a vnitřní proměnné do jednotlivých řádků pravdivostní tabulky. Obvykle je vhodné nejprve v její horní části na jednotlivých sloupcích postupně vypsat všechny možné kombinace vstupních a vnitřních proměnných a přiřadit jim požadované hodnoty proměnných výstupních. Potom do jednotlivých sloubců vepíšeme i zavedené kódy vnitřních stavů (t_n). Všechny potřebné hodnoty získáme přímým přepisem ze stavového diagramu.

Nakonec stanovíme požadované vnitřní stavy následující fáze, t_n+1. I ty pohodlně zjistíme z kódového obsahu následujícího stavu, tj. toho, na který při splnění všech podmínek v daném sloupci tabulky ukazuje šipka stavového diagramu. Tím máme vyplněnu celou pravdivostní tabulku s výjimkou vnitřních řádků, příslušejících budícím funkcím.

Ve třetí fázi je nejprve třeba odvodit všechny budící funkce. Jejich jednotlivé sloupce v tabulce musí být zaplněny vhodnými kódy, zajišťujícími změnu aktuálního vnitřního stavu (t_n horní strana tabulky) na požadovaný budoucí stav (t_n+1. dolní strana). Konkrétní odvozeni budících funkcí již závisí na typu užitého klopného obvodu (D, J-K). Běžným postupem při řešení kombinačního obvodu (algebra, mapa) lze odvodit minimalizovaný tvar jak budicích, tak výstupních funkci.

Vidíme, že stavový diagram zavádí do řešení sekvenčního obvodu určitý systém. Tento popis není pro pochopení pracovního postupu dostatečné přehledný, byl míněn především jako poznámky k vlastni práci. Následující kapitola je vzorový příklady řešení návrhu stavového automatu. Příklady jsou zvoleny extrémně jednoduché proto, aby řešení mohlo být sledováno bez větších problémů.