Zdroj: http://prochazka.clanweb.eu/index.php?a=knihovnicka/karnaughova-mapa-dvou-promennych • Vydáno: 12.1.2008 14:59 • Autor: hacesoft
Nejjednodušší je zápis mintermu, tj. jedné položky pravdivostní tabulky nebo funkce UDNT. Jako příklad zapíšeme minterm /AB, který má hodnotu 1. Po obvodu mapy vyhledáme odpovídající souřadnice /A, B a do políčka, které je jejich průsečíkem, zapíšeme 1. Postupným vyčerpáním všech položek pravdivostní tabulky nebo funkce UDNT zapíšeme všechna políčka mapy, která mají mít hodnotu 1. Políčka, která mají mít hodnotu 0, nezapisujeme. Příklad zápisu mintermu /AB je na následujícím obrázku.

Pro demonstrační účely použijeme následující tabulku:

Do mapy lze samozřejmě zapsat i obecnou logickou funkci ve tvaru DNT, v niž se libovolná proměnná může vyskytovat nejen jako člen mintermu, ale i v jednoduchém tvaru. V tom případě vyhledáme její jedinou souřadnici a do všech políček příslušného řádku nebo sloupce vepíšeme hodnotu 1. Vytváříme tak již zmíněné sdružené pole, řetězec mintermu. Při výskytu další proměnné v jednoduchém tvaru postupujeme stejně. Mintermy funkce DNT zapisujeme klasickým postupem.
Příklad zápisu funkce A + /AB:
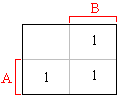
Zapsaná funkce se v mapě dvou proměnných minimalizuje tak, že se snažíme graficky sdružovat všechna (tj. v tomto případě dvě) sousední políčka, která mají vepsanou hodnotu 1. Pokud je to možné, lze při jejich výpisu z mapy vyloučit jednu proměnnou a celá funkce se tím zjednodušuje. Políčka se sdružují tak, že sousední mintermy graficky spojujeme oválem. Jednotlivé ovály, sdružené mintermy podle určité proměnné, se dále navzájem váží, spojují.
Výraz na následujícím obrázku nelze minimalizovat. Sám již představuje svoji nejjednodušší formu.

Postup minimalizace funkce, zapsané z výše uvedené pravdivostní tabulky do mapy ukazuje následující obrázek:
Zápis pravdivostní tabulky:
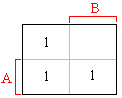
Minimalizace pravdivostní tabulky:
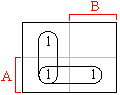
Sdružením dvou dvojic sousedních mintermu A /B + /A /B, A /B + AB získáme dvě jednoduché proměnné. Zjednodušená a v tomto případě už i minimalizovaná funkce je dána logickým součtem obou proměnných, plně určených vždy jednou souřadnicí řádku (A) nebo sloupce (/B). Výsledná funkce Y = A + /B je shodná s výsledkem algebraického řešení.
Rozvoj funkce až do úrovně UDNT jsme již vlastně dělali. Bylo to při zápisu funkce logického součtu dvou jednoduchých proměnných A + B. Abychom tuto funkci mohli zapsat, rozložili
jsme ji na jednotlivé mintermy. Můžeme jistě dobře porovnat zjednodušení, které mapa přináší ve srovnání s postupem podle Shannona. Postup při rozvoji je tedy přesně opačný než při minimalizaci:
Do všech sdružených mintermu podle řádku nebo sloupce zapíšeme 1. Rozvinutá funkce UDNT je pak rovná logickému součtu jednotlivých nalezených mintermu.
UDNT (A +B) = AB + A /B + /AB
Inverzi logické funkce, ekvivalentní algebraickému postupu, lze výhodně řešit pomocí mapy. Znamená to pouze opačné vyhodnotit, negovat hodnoty jednotlivých mintermu mapy, tedy zaměnit 0 až 1 a opačně. Pouze pro názornost je na následujícím obrázku znázorněna inverzní mapa logického součtu A + B.
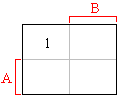
Ve skutečnosti ji ovšem vůbec nekreslíme, ale pouze opačně vyhodnotíme zápis mapy v přímém tvaru.