Zdroj: http://prochazka.clanweb.eu/index.php?a=knihovnicka/karnaughova-mapa-pro-tri-promenne • Vydáno: 12.1.2008 15:05 • Autor: hacesoft
Zápis pro tři proměnné se od mapy pro dvě proměnné liší tím, že její pole je ve skutečnosti třírozměrné - jednotlivé mintermy si můžeme představit jako vrcholy krychle. Plošné znázornění všech tří typů Karnaughových map je maximálně výhodné, musí však být bráno v úvahu při hodnocení sousednosti mintermu. Na rozdíl od dvourozměrného typu mapy je u mapy tří proměnných nutno považovat ze sousední i ti, které sice jako sousední zakresleny nejsou, ale leží na vzájemně protilehlých okrajích mapy. Jsou to tedy políčka /A /B /C - /A /B C a A /B /C - A /B C.
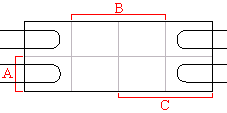
Jejich sousednost ostatně ukazuje i vzájemná odlišnost inverzí jedné proměnné. Mintermy v mapě sdružujeme do souvislých polí se dvěma nebo čtyřmi prvky.Tím můžeme vyloučit jednu nebo dvě proměnné. Následující obrázek ukazuje jednoduchý příklad zjednodušení funkce, jejíž všechny mintermy se nacházejí ve vzájemně protilehlých políčkách. Výsledkem minimalizace je jediná proměnná.
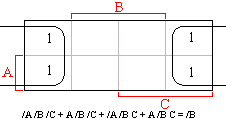
Máme zapsat a pomocí mapy minimalizovat funkci:
/A (B + C) + A /B C + A /B /C
Výraz v závorce představuje funkci výhradní (exkluzivní) součet.
Abychom mohli funkci zapsat do mapy, musíme ji upravit do tvaru DNT odstraněním závorek. Současně odstraníme operátor výhradního součtu rozpisem funkce (B + C) = B /C + /BC.
Potom bude mít upravená funkce tvar:
/A B /C + /A /B C + A /B C + A /B /C.
Pro zajímavost si všimneme, že původní funkce není zadána v optimálním tvaru. V součtu
posledních dvou konjunkcí by bylo možno odstranit proměnnou C, protože A /B C + A /B /C = A /B.
My tuto možnost klidně přehledneme, protože při zápisu do mapy není podstatná.
Zápis upravené funkce do mapy i její minimalizace ukazuje následující obrázek.
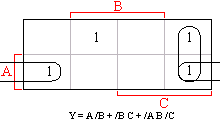
Výsledná minimalizovaná funkce má tvar:
A /B + /BC + /A B /C.
Při řešení funkce pomocí logických hradel může být naznačená následující úprava užitečná.
Lze například vyloučit potřebu vyjádření exkluzivního součtu úpravou minimalizovaného tvaru na výraz
/B (A + C) + /A B /C, nebo /B (A + C) + B /(A + C) apod. Stejně užitečné může být určit inverzní funkci, ať už přímou negací
minimalizované funkce, tj. /( /BC + A /B + /A B /C), nebo pomocí inverzní mapy. Pak získáme druhý, duální tvar inverzní funkce AB + BC + /A /B /C.
Inverzí této funkce pomocí Shannonova teorému můžeme odvodit duální konjunkční tvar přímé funkce (/A + /B) (/B + /C)( A + B +C). Všechny tyto možnosti mohou být v praxi užitečné.