Zdroj: http://prochazka.clanweb.eu/index.php?a=knihovnicka/sekvencni-obvody • Vydáno: 12.1.2008 15:12 • Autor: hacesoft

Sekvenční obvody

Kombinační logika a odpovídající logické členy jsou skutečným základem číslicové techniky. Jejich samostatné využiti je však značně omezené: Každá probíhající činnost (proces) se ve skutečnosti skládá z posloupnosti (sekvence) dílčích, elementárních činností, akcí. Kombinační obvod může vykonávat právě jen tuto elementární činnost. Posloupnost jednotlivých akcí umožňují definovat sekvenční obvody. Jejich funkce v sekvenční síti je však zcela odlišná. Obvodová struktura musí být řešena tak, aby se uplatnil časový rozměr, musí se používat paměťové prvky, které si nějakým způsobem pamatují předchozí stav. Jen tak lze rozhodovat, jaká akce má po právě vykonané následovat, jen tak lze definovat a řídit konkrétní proces, byt i zcela jednoduchý. Vhodnou vzájemnou součinností kombinační a sekvenční logiky lze vytvořit technické prostředky, které realizaci takového procesu umožňují. Řekli jsme, že principem sekvenční funkce, sekvenční logiky, je uplatnění paměťového prvku v logické síti. Paměťové chování logického obvodu lze dosáhnout různými způsoby. Vždy se však jedná o nějaké uplatněni zpětné vazby, způsobující, že vlastní obvod nepůsobí v závislosti na vstupních signálech pouze směrem "ven" na výstup, ale i sám na sebe. Tím v určitém čase nabývá specifického, tzv. vnitřního stavu. Podle něj pak reaguje (změněným způsobem) na vstupní proměnné v čase následujícím. V tom pák opět nabývá nového vnitřního stavu, vytváří se nová podmínka pro reakci obvodu na vstupní proměnné atd. V nejjednodušších sekvenčních obvodech se pro zavedeni paměťového členu používají např. i běžné články RC (monostabilní klopný obvod). Další časté použití nachází ve stejné, tentokrát staticky definované funkci známý obvod R-S. Rozsáhlejší obvody ovšem s využitím jednoduchých obvodů R-S řešit nelze, složitost jejich návrhu by mnohonásobně překračovala únosné meze. Aby vůbec bylo možno přistupovat k návrhu obecného sekvenčního obvodu systematickým způsobem, je nutno vycházet z principu synchronizace všech vzájemně navazujících stavů. Tato synchronizace se v číslicové technice zajišťuje zavedením synchronizačního, hodinového signálu. Je většinou jednoduchý, někdy však i dvou nebo několikafázový. Celá sekvence elementárních akcí je tak periodickým vzorkováním rozdělena na stejné dlouhé (ekvidistantní) časové úseky, z nichž vždy jeden právě existující (t_n) a druhý navazující (t_n+1) jsou vyhodnocovány a registrovány pouze v okamžiku výskytu hodinového impulsu. Pro tyto aplikace byly postupným vývojem odvozeny od obvodu R-S některé další, dnes již standardní typy klopných obvodů. Jejich společným rysem je to, že jsou synchronní. Jejich činnost je řízena taktem hodinového signálu. Jedná se především o klopné obvody typu D, J-K a Master/Slave J-K. Mezi nimi se pak ještě rozlišuji obvody se statickým a dynamickým datovým přístupem. Rozborem jednotlivých typů klopných obvodů se zabývat nebudeme. Pomíjíme je stejně jako fyzikální principy a vnitřní struktury logických hradel. Důvodem je hlavně to, že se jedná vesměs o záležitosti dobře známé, a také skutečnost, že jsou probírány v každé příručce číslicové techniky. Kdo však má v této oblasti mezery, měl by se je snažit odstranit. Pro práci se složitějšími sekvenčními obvody je dobrá znalost funkce uvedených klopných obvodů nutná. Níže jsou pouze pro další potřebu uvedeny obecné pravdivostní tabulky klopných obvodů D a J-K.

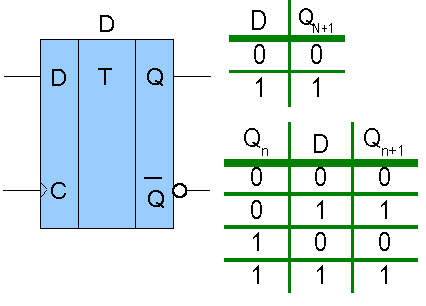
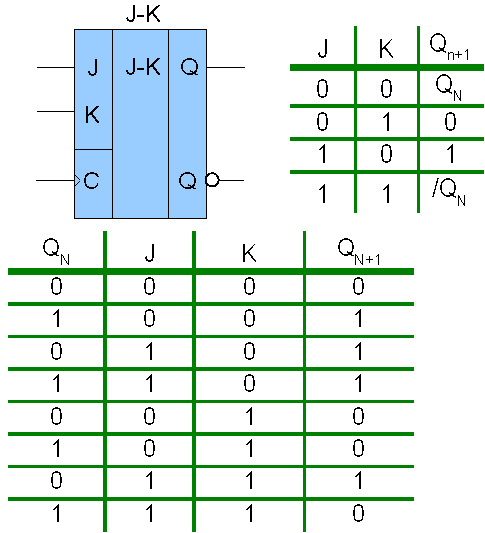
Běžné tvary pravdivostních tabulek a rozepsané tvary sekvenčních funkci pro všechny kombinace vstupních proměnných a vnitřních stavů.

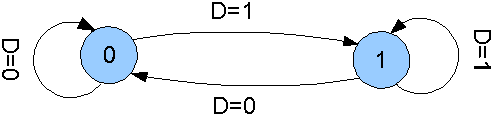
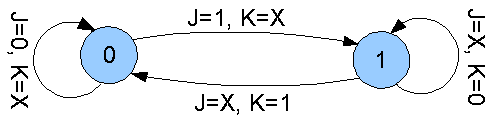
Odpovídající stavové diagramy.

Je jistě zcela evidentní, že návrh sekvenčních obvodů musí být ve srovnáni s kombinačními obvody již z principu mnohonásobně složitější. Sekvenční obvod musí nejen v každém okamžiku požadovaným způsobem reagovat na aktuální logické úrovně vstupních a vnitřních proměnných (stavů), ale navíc musí vždy vytvářet nové vnitřní stavy tak, aby činnost při následujícím taktu opět za všech vnějších podmínek jednoznačně definovala požadované výstupní akce.

Odpovídající vícerozměrnou funkční strukturu obvodu nelze, při jen poněkud větší složitosti, jednoduše či přehledně definovat ani popsat algebraickými, tabulkovými nebo grafickými metodami. Každý dnes již jistě máme své zkušenosti například s časovým diagramem, často používaným při řešení jednoduchých obvodů. I když je časový diagram velmi užitečnou praktickou pomůckou, sám o sobě dokonalý postih obecného sekvenčního obvodu neumožňuje. Existuje poměrně jednoduchá metoda řešení synchronizovaného sekvenčního obvodu, kterou lze doporučit pro praktické aplikace. Je založena na důsledném odděleni vnějších, již zmíněných vstupních a výstupních proměnných, které jsou při zahájeni návrhu známé, od vnitřních proměnných, které je třeba vyřešit. Vzájemné relace vnějších a vnitřních proměnných jsou pak podkladem pro řešení obvodu. K tomu se přistupuje na základě odvozených budicích a konverzních funkcí. Zatímco následující obrazek popisuje vnější proměnné,

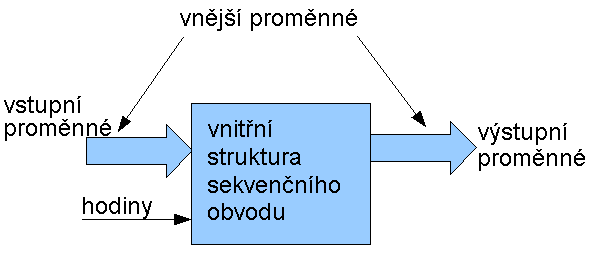
Vnitřní struktura obecného sekvenčního obvodu.

následující obrázek je zobecněná vnitřní struktura sekvenčního obvodu.

Vnitřní struktura obecného sekvenčního obvodu s vyznačením vnitřních proměnných.

Ta se skládá zhruba ze tří bloků:

paměťový blok slouží k definici a uchování vnitřního stavu obvodu, vzorkovaného v čase t_n
vstupní kombinační blok vyhodnocením relaci vnějších vstupních proměnných a vnitřního stavu (t_n) nastavuje budíc funkce klopných obvodů paměťového bloku tak, aby byl definován požadovaný vnitřní stav obvodu v okamžiku příštího intervalu, vzorkovaného v čase f_n+1.
výstupní kombinační blok zajišťuje vyhodnocením relaci ustálených (tedy synchronizovaných) vnějších vstupních proměnných a vnitřního stavu požadované stabilní úrovně výstupních proměnných po celý platný interval t_n.

V konkrétních případech mohou některé funkční bloky nebo dokonce i některé signály v naznačené sekvenční struktuře chybět. Jsou to například oba kombinační bloky nebo vstupní proměnné. V každém případě však musí mít obvod nějakou formou vyjádřen paměťový blok a alespoň jeden vnitřní budící signál. Existence alespoň jedné výstupní proměnné je z hlediska aktivního uplatněni sekvenčního obvodu samozřejmostí. Další metody řešení obecného sekvenčního obvodu je kombinací nekolika metod. V první fáze spočívá v interaktivním vytváření stavového diagramu a pravdivostní tabulky obvodu. Z tabulky se pak pomocí binární algebry nebo Karnaughovy mapy odvozuje minimální forma vnitřní a výstupní logiky obvodu. Metoda dokonale postihuje všechny existující kombinace vnitřních stavů obvodu a vnějších proměnných. To sice obvod dokonale popisuje za všech situací, avšak, zvláště při větším počtu stavů a proměnných, dělá jak popis, tak řešení obvodu složitým a nepřehledným. Kombinovaná forma při zápisu řešené úlohy je velmi výhodná: graf umožňuje postihnout všechny akce, vycházející z libovolného vnitřního stavu, tabulka popisuje všechny podmínky potřebné ke každé takové akci. Ani graf, ani tabulka však nedávají obecně přímý přehled o časovém průběhu dílčích akci, obdobný časovému diagramu. Důvody: možné větvení sledu akcí podle vstupních proměnných a chybějící časové měřítko. Proto metoda sama o sobě neumožňuje postihnout hazardní stavy (např. asynchronní čítače). Tomu se bráníme synchronizací vnějších a vnitřních proměnných nebo, někdy, odvozením dílčích časových diagramů z grafu a tabulky.